3.1 : Les graphes
I - Représentation des relations sociales au sein d'un groupe
1) S'informer : Paternité du terme "réseau social"
On attribue à J. A. Barnes, anthropologue britannique, la paternité du terme “Réseau social” en 1953. Il en propose même une représentation.
« L’image que j’ai en tête est celle d’un ensemble de points qui sont reliés par des lignes. Les points de cette image sont des individus, ou parfois des groupes, et les lignes indiquent quelles sont les personnes qui interagissent les unes avec les autres. »
2) Représentation des relations sociales de la classe
Suivre les indications du professeur.
3) Lien avec les réseaux sociaux numériques
1) Citer les réseaux sociaux que vous connaissez.
2) Quelle représentation pourrait-on utiliser pour le réseau social Facebook ?
3) Quelle représentation pourrait-on utiliser pour le réseau social Twiter ?
II - Notion de graphe
1) Appliquer pour découvrir
On considère le groupe d'amis schématisé ci-dessous :
1) Combien de personne le groupe contient-il ?
2) Quels sont les amis de Bryan ?
3) Denis et Camel sont-ils amis ?
4) Quel semble être la personne centrale du groupe ?
2) S'informer et connaitre : vocabulaire
Un graphe est ensemble de sommets (ou nœuds) et d'arêtes (ou arc pour les graphes orientés).
Un graphe est orienté si les arêtes ont un sens (dans ce cas, on parle plutôt d'arc), dans le cas contraire il est non orienté.
Pour les graphes non-orientés :
- - Chaîne de sommets (ou chemin) : Une chaine de sommets est une suite de sommets consécutifs.
- - Distance entre deux sommets : La distance entre deux sommets est le plus petit nombre d'arêtes qui permet d'aller d'un sommet à l'autre.
- - Excentricité d'un sommet : L'excentricité d'un sommet est la plus courte distance entre ce sommet et les autres sommets du graphe.
- • Diamètre d'un graphe : Le diamètre d'un graphe est la plus petite distance qui permet de relier n'importe quels sommets du graphe.
- • Centre d'un graphe : Le centre d'un graphe est le sommet qui a la plus petite excentricité.
- • Rayon d'un graphe : Le rayon d'un graphe est l'excentricité du centre du graphe.
Un graphe peut être représenté :
- - soit par un schéma
- - soit par une matrice d'adjacence (c'est-à-dire un tableau dont les lignes et les colonnes sont les nœuds).
Exemple :
| Adèle | Bryan | Camel | Denis | |
|---|---|---|---|---|
| Adèle | X | 1 | 1 | 1 |
| Bryan | 1 | X | 0 | 1 |
| Camel | 1 | 0 | X | 0 |
| Denis | 1 | 1 | 0 | X |
3) Appliquer pour comprendre
Dans cette application, on considérera que les amitiés sont symétriques, c'est à dire que si Paul est ami avec Jeanne alors Jeanne est amie avec Paul.
Les amitiés d'un petit groupe peuvent être décrites ainsi :
- - Ashley est amie avec Benoit, Dido et Ela
- - Benoit est ami avec tout le monde
- - Cédric est ami avec Benoit et Ela
- - Dido est ami avec Ashley et Benoit
- - Ela est amie avec Ashley, Benoit et Cédric
1) Représenter le graphe correspondant aux amitiés de ce groupe sous la forme d'un schéma.
2) Donner le nombre de nœuds du graphe.
3) Donner le nombre d'arêtes du grape.
4) Déterminer l'excentricité de chaque nœud.
5) En déduire le centre du graphe.
6) Indiquer le diamètre du graphe.
7) Représenter le graphe sous la forme d'une matrice d'adjacence.
4) Un outil en ligne pour représenter des graphes
Ouvrir la page : https://viz-js.com/.
Pour les curieux, la documentation compète du langage se trouve ici : https://graphviz.org/documentation/
4.a) Observer et comprendre
1) Coller le code ci-dessous dans la partie gauche et observer le graphe obtenu.
graph monGraphe {
node[shape=circle fillcolor="#eeeeee" style=filled]
A -- {B C D}
B -- C
}2) Coller le code ci-dessous dans la partie gauche et observer le graphe obtenu.
graph monGraphe {
layout=circo
bgcolor="none"
node[shape=egg fillcolor="#666666" style=filled fontcolor="#ffffff"]
Raymond -- Adeline
Raymond -- Jean
Raymond -- Sophie
Gaston -- Alfred
Alfred -- Adeline
Alfred -- Sophie
Adeline -- Jean
}4.b) Appliquer
Dans l'application en ligne viz-js.com, écrire le code du graphe ci-dessous. Une fois le bon code obtenu, le coller dans votre compte rendu.
III - Exercices
Exercice 1
Reprendre le graphe du II.4.A et répondre aux questions suivantes :
1) Déterminer l'excentricité de chaque nœud.
2) En déduire le centre du graphe.
3) Indiquer le diamètre du graphe.
Exercice 2 : Matrice d'adjacence
On considère le graphe représenté par la matrice d'adjacence ci-dessous :
| Adèle | Bryan | Camel | Denis | Elfie | Flynn | |
|---|---|---|---|---|---|---|
| Adèle | 0 | 0 | 0 | 1 | 1 | 1 |
| Bryan | 0 | 0 | 1 | 0 | 0 | 0 |
| Camel | 0 | 1 | 0 | 1 | 0 | 0 |
| Denis | 1 | 0 | 1 | 0 | 0 | 1 |
| Elfie | 1 | 0 | 0 | 0 | 0 | 0 |
| Flynn | 1 | 0 | 0 | 1 | 0 | 0 |
1) Représenter le graphe par un schéma.
2) Indiquer le diamètre du graphe.
Exercice 3 : Un petit groupe d'amis
Alban, Béatrice, Charles, Déborah, Eric, Fatima, Gérald, Hélène sont inscrits sur le même réseau social.
Alban est ami avec Béatrice, Déborah, Eric et Fatima.
Béatrice est amie avec Alban, Charles, Déborah, Eric et Gérald.
Charles, lui, est ami avec Béatrice, Déborah et Hélène.
Déborah est amie avec Charles, Béatrice, Alban et Gérald.
Eric, avec Béatrice et Alban, Fatima, avec Alban, Gérald et Hélène.
Gérald, avec Béatrice, Fatima, Eric et Hélène et Hélène, avec Charles, Eric, Fatima et Gérald.
1) Qui a le plus d’amis ? le moins ?
2) Tous les participants ont-ils des amis en commun ?
3) Tous les participants peuvent-ils entrer en contact par le biais de leurs amis ?
4) Représenter le graphe de ce groupe (on considérera que les amitiés sont symétriques).
5) Quel semble être le centre du graphe.
6) Indiquer le diamètre du graphe.
Exercice 4 : Hamlet de Shakespeare
La Tragique histoire d'Hamlet, prince du Danemark est probablement la tragédie de William Shakespeare (1564-1616) qui a fait couler le plus d'encre, tant est grand le pouvoir de fascination de son héros. C'est une pièce complexe, foisonnante, qui s'inscrit dans le contexte de la « tragédie de vengeance ».
L'une des analyses possibles consiste à établir le graphe des relations entre les personnages de l'œuvre.
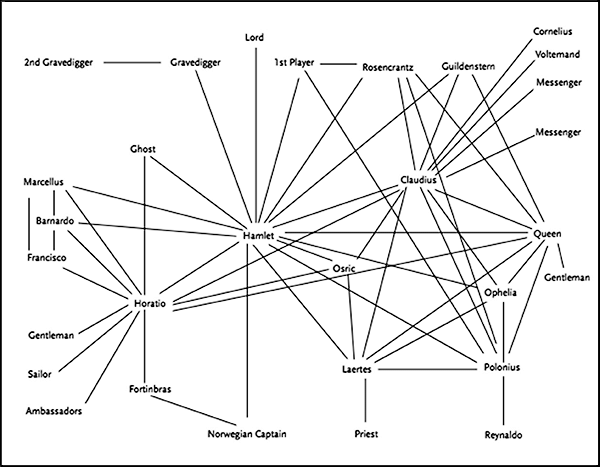
1) Indiquer le nombre de personnage du livre.
2) Déterminer la distance entre Horatio et Reynaldo.
3) Déterminer l'excentricité de Claudius.
4) Indiquer le centre du graphe.
5) Déterminer le diamètre du graphe.